Quote:
The way to do this is to formulate the theory in terms of a hypothesis which can be tested, then test it.
The hypothesis is that, up to 1993, there was a falling `trend' in road casualties; and after 1993, this `trend' slowed. 1993 is important here because it was the year in which speed cameras were first introduced. (It was also -- coincidentally -- the year when the amount of traffic on the roads began rapidly to increase after a hiatus during the recession of the early 1990s. Make of this what you will. In any case to do this properly the analyst would have to show that 1993 was a significant year; but here we're only testing previous claims, so we skip that step.)
Clearly, the number of road casualties in any given year is the result of a random process. By saying that there is a `trend', we are claiming that the number of deaths in a given year is given by some smooth function which changes slightly year-on-year -- the trend -- plus some random variable, a `residual'. Here are some possible models:
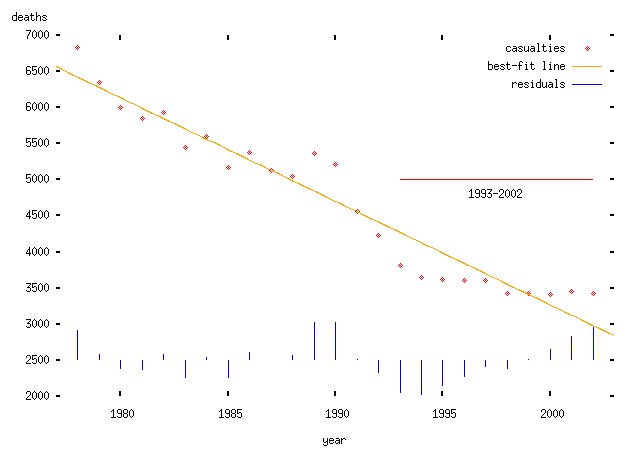
Linear trend: we assume that the mean number of deaths in any given year is some constant fewer than the mean number in the preceding year. Obviously this model is wrong at some point, since the number of deaths must be positive or zero; but for a short interval this may be a valid model:
 Exponential model
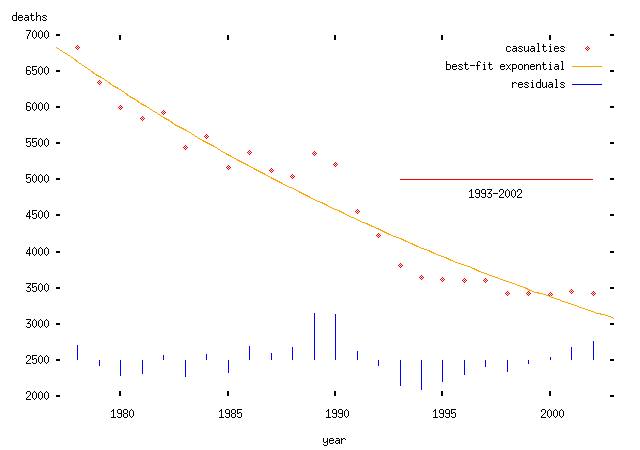
Exponential model: we assume that the mean number of deaths in any given year is some constant fraction less than the mean number in the preceding year. This has the nice property that it can never be negative.
(
Note that I haven't justified why there should be a downward trend or why it should be linear or exponential. If I wanted to make some kind of positive prediction, I would need to do so; in particular, I would need a model of why this should happen. But I don't need to do that here, since I'm interested in analysing somebody else's claim, which itself assumes a particular trend. To do anything useful with this kind of trend, you really need a theory which explains why there should be a trend and what form it takes. There's also the issue of how you find the trend. In the ABD's case, they appear to have chosen the trend line which is most favourable to their theory; in the plots above I have used the conventional procedure: to find the best fitting curve or line using a least-squares procedure. The two models fit about equally well, but that's not really relevant since we haven't explained why we would expect such a trend in the first place. I should say that I do believe that there is a trend -- but I can't explain exactly why there is a trend. I expect that it relates to increasing road and vehicle safety, though there are other possibilities.)
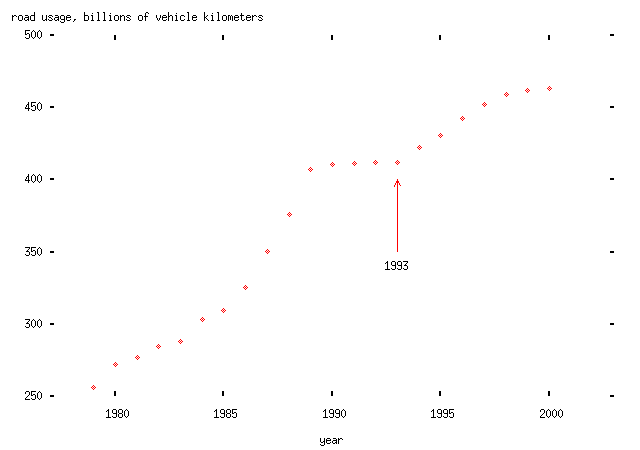
Another theory which is also popular, and which I'm also not going to try to justify, is that road casualties depend linearly on the amount of road traffic -- measured in vehicle kilometers, so that two movements of one kilometer by different vehicles counts the same as one movement of two kilometers by one vehicle -- and fall according to some trend. (This theory is obviously partly sensible -- increasing road usage will, presumably, lead to more accidents -- but the assertion about linear dependence would need to be tested for this theory to be very useful. In particular, a nonlinear dependence would be easier to justify, since motorists often crash into one another rather than into stationary objects, and the rate at which that occurred would presumably depend upon the square of the number of vehicle kilometers driven.)
Anyway,
here's the rate of road usage in vehicle kilometers on Britain's roads from 1993 to 2000 (note the increase starting after 1993):
... and here's the plot of deaths per vehicle kilometer driven with an exponentially-falling trend:
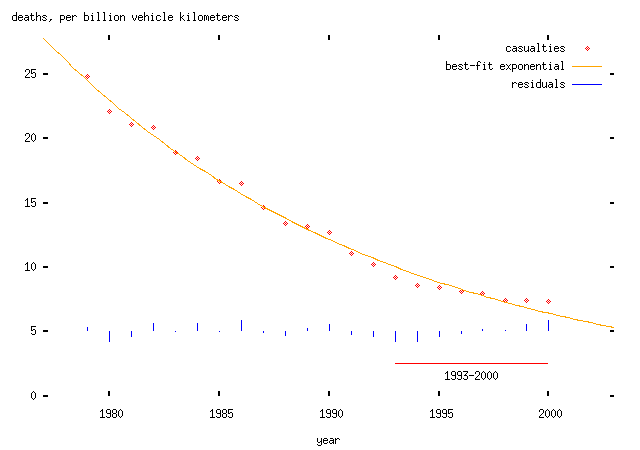
(Superficially, I'll remark that this looks pretty good. But that doesn't necessarily mean anything much.)
Now we want to ask whether these `trends' changed after 1993. We can't do this just by looking at the plots, because a pattern that appears to be obvious to the eye might just be coincidental. Instead, we need to do some kind of formal test to find out whether the `trend' has changed.
If the trend had indeed changed, the residuals after 1993 would be distributed differently from those before 1993. Either the variance -- i.e., the spread -- of the residuals would increase; or, more interestingly, the mean of the residuals would change. In English, that means that the trend would consistently under- or overestimate the actual number of deaths. (The anti-speed-camera people would like to say that the trend has underestimated the number of deaths, and interpret this as evidence that some change -- speed cameras -- `caused' the extra deaths.)
A standard technique to answer this question is a Kolmogorov-Smirnov test (like everything in statistics, it's named after its inventors); this test can be used to tell us whether two sets of samples -- in this case, the pre- and post-1993 residuals from the various models -- are either (a) drawn from different distributions; or (b) are consistent with having been drawn from the same distribution. The idea of this test is that we take the two cumulative distributions and plot them on the same axes, and then find the furthest distance between the two curves. This maximum distance (called the `Kolmogorov-Smirnov test statistic') can then be compared to a critical value which tells us whether the two sets of samples were drawn from different distributions or not. (Surprisingly enough given my description, this is actually formally correct and backed up by all sorts of hideous maths.) Here's an illustration with the residuals for the exponential case above:
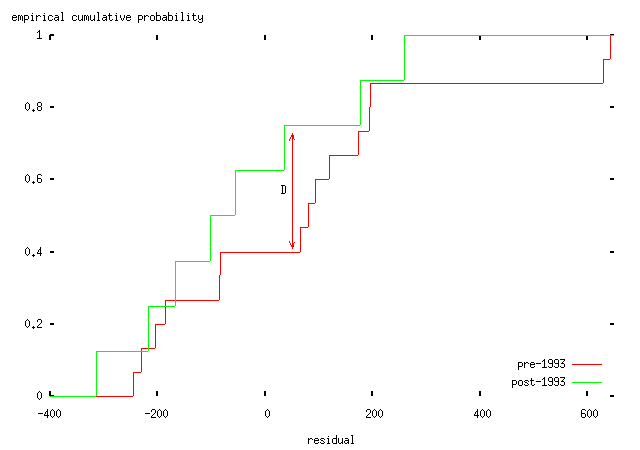
Pleasingly, those nice people at the R Project have implemented software which will do almost all of the work for us. So:
Model K-S statistic p-value Conclusion
linear, total deaths 0.1806 0.9718 same distribution
exponential, total deaths 0.3403 0.4059 same distribution
exponential, deaths per vehicle kilometer 0.1714 0.9943 same distribution
-- that is, in each case, there is no evidence that the trend is any worse a fit after 1993 than before. None of these data support the hypothesis that there was a change in trend in road casualties in 1993, measured either in total or per vehicle kilometer.
This doesn't, of course, tell us anything new about speed cameras, or whether they are good or bad for safety. It tells us that one argument used against them -- by the ABD, and Idris Francis and other assorted loons from the `Safe Speed' campaign -- is bull.



